In science we are often rediscovering the already known, this happens on a personal level almost every day. You feel dumb and insecure, surrounded by the condensed wisdom of lifetimes in science, textbooks of seemingly impenetrable theories whose every page requires hours of study to have the merest glimpse of the knowledge within.
Recently I’ve been trying to think about how to represent the alignment of a stick within a cube (the Methyl-Ammonium in MAPI perovskite, to interpret some Ab-initio Molecular Dynamics). Obviously there is some odd symmetries at play here, there are 8 corners to a cube, 6 faces and 12 edges. This must have a point group associated with it (and the cubic groups are O and Oh). But I couldn’t make sense of the character tables, into how to turn this into an algorithm to recast an arbitrary vector onto its unique domain.
So I just sat and thought, wrote scribbles and sat knowing, for certain, that this was something simple and well understood, yet not knowing how I could understand.
After all this - thinking of symmetries, and how to collapse the basis vectors (by arithmetic and rotating my pen within an imaginary cube); and I’d arrived back at a representation of the Oh group, gratifyingly the symmetry had the correct fold and even the ‘Reflection Domain’ matched the beautiful Wikipedia render.
Once I’d hauled myself up to the merest hint of the beauty of 18th Century mathematics that is trivial group theory (or rather, just using the character tables), I had a method to attack a problem I was working on.
If you want to reduce the d=x,y,z coordinates to their cubic symmetry, simply sorted(abs(d)). (The abs reflects in the basis vectors, to select 1/8th of the cube, and the sorted() gives you the three-planes of mirror symmetry to produce the correct representation of edges, faces and corners. I justified this that since orientation doesn’t matter you must be able to change sign of the basis; and as the basis vectors are equivalent, you must be able to reorder them.)
With no symmetry, the signal to noise is low, and what you see are a lot of artefacts from the starting configuration
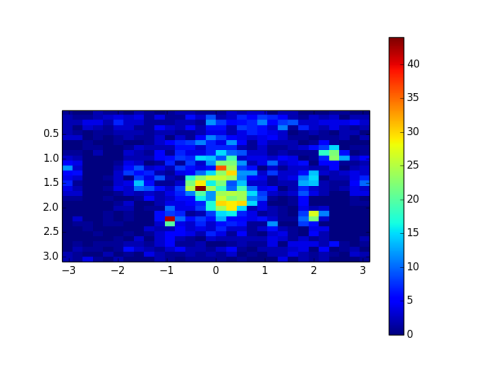
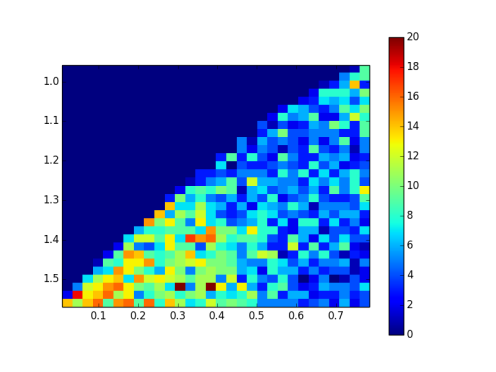
But when you fold back the 48 equivalent areas to a single one, bonza - some actual data!
http://www.youtube.com/watch?v=8Wb0V-68Kao
Nb: ‘Whiteboard’ process of poor camera phone shot of my notebook via https://gist.github.com/lelandbatey/8677901, convert "$1" -morphology Convolve DoG:15,100,0 -negate -normalize -blur 0x1 -channel RBG -level 60%,91%,0.1 "$2".

