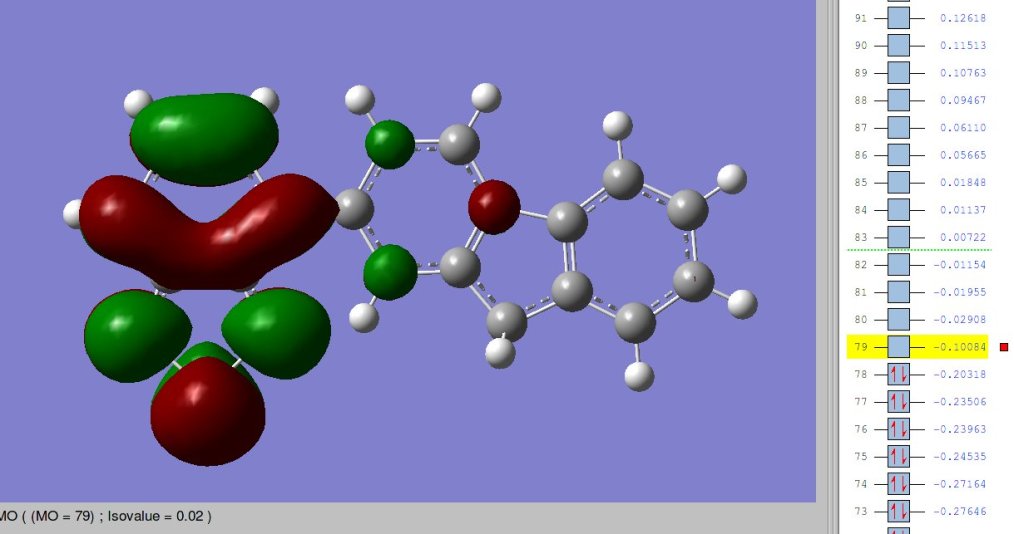
A colleague recently asked about assessing the Donor-Acceptor strength of a given polymer by Quantum Chemical calculation. Often the literature just seems to print the pretty electron spin density plots from Gaussian at an arbitrary isovalue, then essentially relying on just making a statement about the 2D area occupation of this plot!
I was interested in whether one could find a simple method of putting this on a more quantitative basis. The obvious starting point is a simple Mulliken population analysis, and the simplest method & tool that I found for this was to use Gausssum, a quantum chemical log file python based analysis program, to produce partial densities of states for the molecule.
The extra requests you add to your Gaussian COM file is ‘pop=full’ for the population analysis and our old friend iop 3/33=1, to get Gaussian to output the 1 electron orbitals. The Gaussum manual also suggests iop 3/36=-1 to stop Gaussian calculating matrices and making the log file inordinately long.
I was trying with a simple Polyfluorene - BT b3lyp/6-31g* calculation as a test and got figures of:
BT PFO
LUMO: 95% 5%
HOMO: 31% 69%
Certainly seems to show the push pull character in a quantitative manner, and certainly seems more scientific that simply staring at the molecular orbital spin density isovalue shapes as below.
For the PFO-BT dimer, my Groups.txt looked like:
atoms
PFO
1-22
BT
23-34
NB: The Groups.txt file you have to create is rather fragile with Gausssum 2.2.5. For instance, you must not have any extra lines at the end of the file, otherwise you get a crash & a set of incomprehensible python errors!
COM file command line was:
#p b3lyp/6-31g* geom=connectivity pop=full iop(3/33=1,3/36=-1)
Finally, I also did an extremely ‘cheap’ calculation with Zindo (7 seconds!), and got fairly sensible results of:
BT PFO
LUMO: 82% 4%
HOMO: 38% 67%
Ok, so the occupations don’t add to 100%, but as a ratio they agree pretty well with a full hybrid DFT calculation.
Refs:
http://gausssum.sourceforge.net/
http://gausssum.sourceforge.net/DocBook/ch07s02.html - partial density of states information.